这里要介绍的是用Mathematica解微分方程(组),并按照响应的成果,进行相关画图,甚至进步履态模拟。


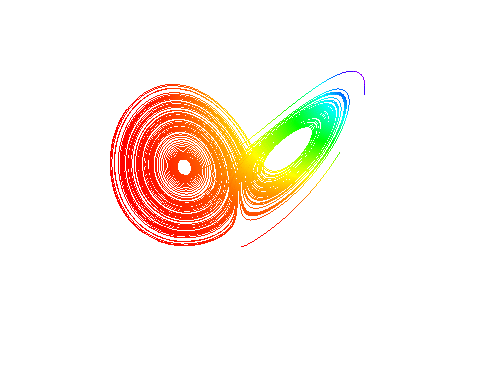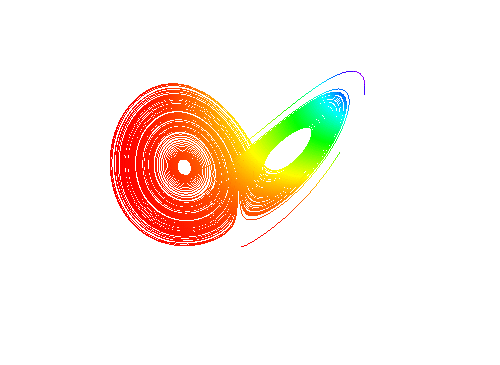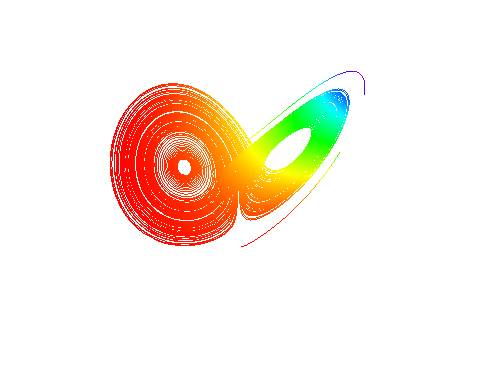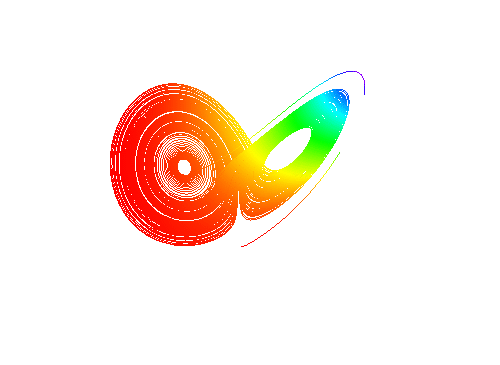
工具/原料
- 电脑
- Mathematica
方式/步骤
- 1
给出微分方程y''(x)+y(x)==1,求其的通解:
DSolveValue[y''[x] + y[x] == 1, y[x], x]
获得的通解是:c2*sin(x)+c1*cos(x)+1。
显然,通解是不成能作出图像的!
可是,我们可以对c1、c2付与分歧的值,再用Show+Table,把所作的图放到一路(注重,年夜写字母C是Mathematica的内部函数,是以,作图的时辰,要把C全数换当作c):
Show[Table[
Plot[1 + c[1] Cos[x] + c[2] Sin[x], {x, -2 Pi, 2 Pi}],
{c[2], -1, 1,0.5}, {c[1], -1, 1, 0.5}]]


- 2
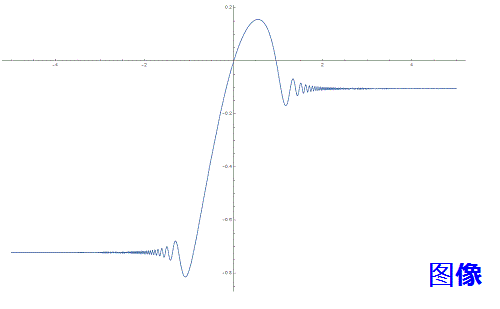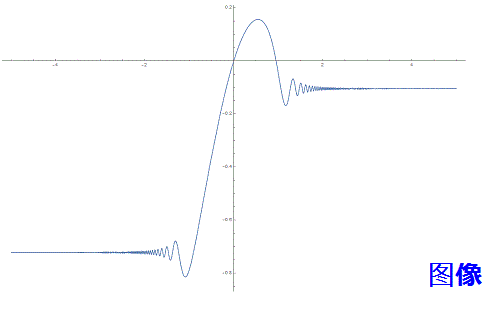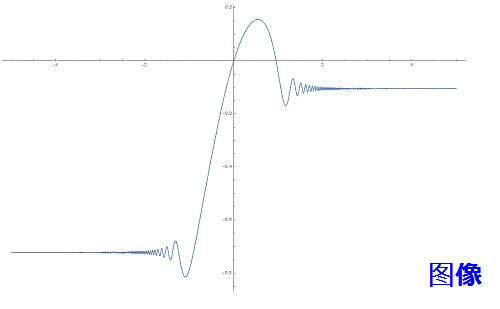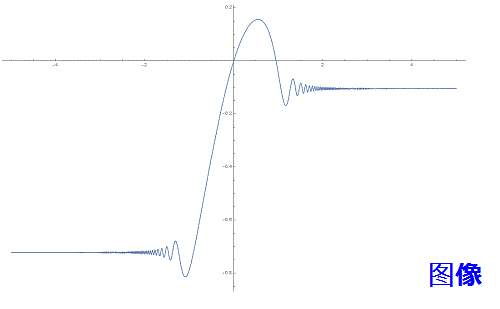
用NDSolveValue 可求出微分方程的数值解(俗称——特解):
NDSolveValue[{y'[x] == Cos[x^6 + x + 1], y[0] == 0}, y[x], {x, -5, 5}]
没有给出公式,可是不故障作图:
Plot[%, {x, -5, 5}]

- 3
求二元微分方程组的特解:
{xsol, ysol} =
NDSolveValue[{
x'[t] == -3 y[t] - x[t]^2,
y'[t] == Sqrt[3] x[t] - y[t]^3,
x[0] == y[0] == 1}, {x, y}, {t, 100}]
把成果作为参数方程,来进行作图,这是混沌现象:
ParametricPlot[{xsol[t], ysol[t]}, {t, 0, 100}]

- 4
用互动结果演示一下上图的作图过程:
Manipulate[ ParametricPlot[{xsol[t], ysol[t]}, {t, 0, a}], {a, 0.01, 100}]
Manipulate[ ParametricPlot[{xsol[t], ysol[t]}, {t, 0, a}], {a, 0.01, 100,0.1}]
Manipulate[ ParametricPlot[{xsol[t], ysol[t]}, {t, 0, a}], {a, 0.01, 10,0.001}]



- 5
这个让我想到了闻名的“Lorenz吸引子”,需要知足的微分方程组是:
x' (t)=-10(x(t)+y(t) )
y' (t)=x(t)(-z(t) )+28x(t)-y(t)
z' (t)=x(t)y(t)-(8z(t))/3
“Lorenz吸引子”的每一个点由{x(t),y(t),z(t)}确定,t是时候参数。我们先来解出{x(t),y(t),z(t)}当x(0)=z(0)=0,y(0)=1时的数值解:
NDSolve[{x'[t] == -10 (x[t] - y[t]),
y'[t] == -x[t] z[t] + 28 x[t] - y[t],
z'[t] == x[t] y[t] - (8/3) z[t],
x[0] == z[0] == 0, y[0] == 1},
{x, y, z}, {t, 0, 200}, MaxSteps -> Infinity]

- 6
然后在三维空间里,画出它的图像:
ParametricPlot3D[Evaluate[{x[t], y[t], z[t]} /. %], {t, 0, 200},
PlotPoints -> 50000]

注重事项
- 关于微分方程的相关理论十分丰硕,这里仅仅是涉及到一点“外相”,远远不克不及解决年夜大都问题。
- 今后,再慢慢的深切进修吧!