判断3个整数乘法等式在几进制成立怎样用C++实现

肆意给你一个表达式m×n=p，请判定它在几进制下当作立，进制在二进制与16进制之间，例如7×8＝62在十进制下不当作立的，但在9进制下是当作立的，若是等式有多种进制当作立，则选择进制小的输出。若是等式没有当作立的进制，则输出等式无法当作立。

工具/原料

• C++

方式/步骤

1. 1

   输入数据时，第1行输入3个整数，每个整数位数小于7位。

   输出数据时，当有等式当作立的进制时，输出知足前提的最小进制。

   若是等式无法当作立，则输出等式无法当作立。

   
2. 2

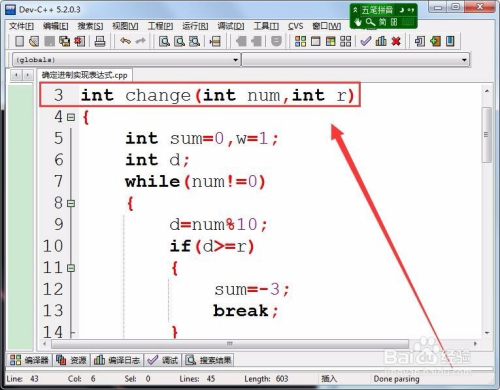
   首先，界说一个函数，将整数转化为某一进制的值。

   
3. 3

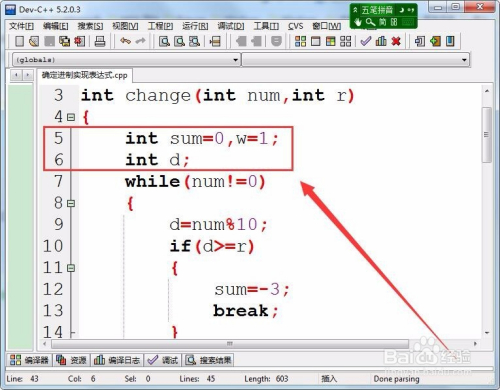
   自界说函数中，界说了三个内部整型变量。

   
4. 4

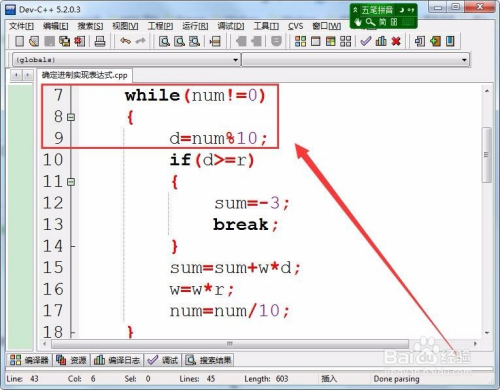
   当整数num不等于0时获取整数的个位值，保留在变量d中。

   
5. 5

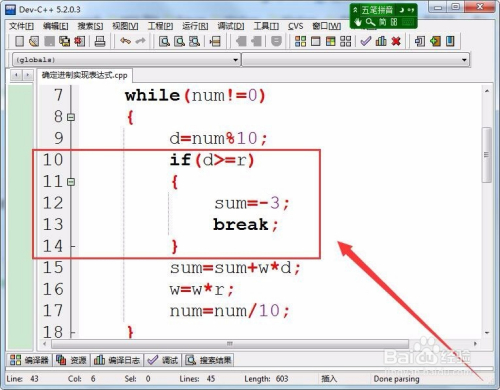
   若是d的值年夜于进制，则转换的值为－3。

   
6. 6

   将整数num转换为响应进制的数值，保留在变量sum中。

   
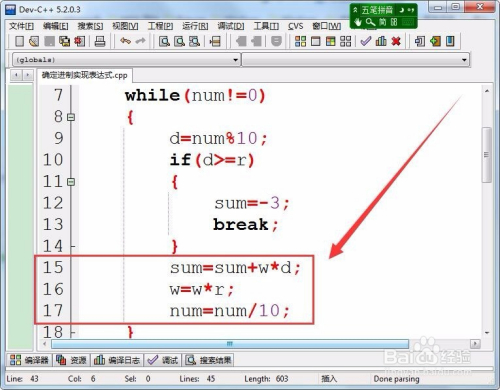
7. 7

   自界说函数输出计较的值，用return返回。

   
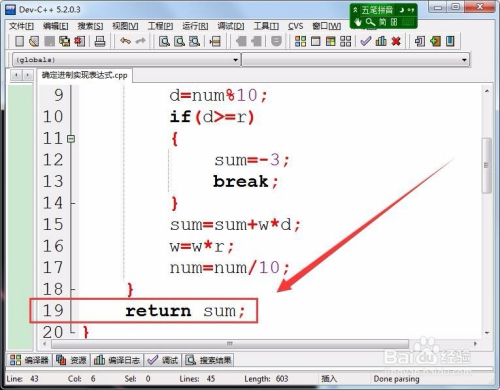
8. 8

   本家儿函数中，界说7个整型变量，保留输入的三个整数、节制轮回的变量，以及将三个整数转换为对应进制后的值。

   
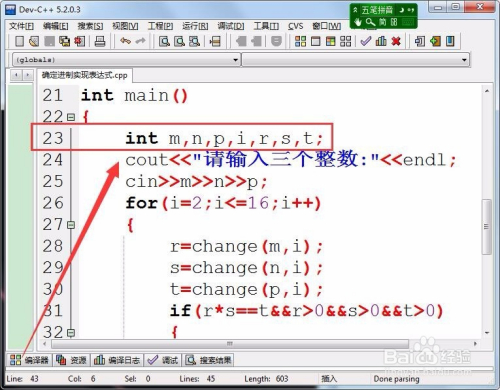
9. 9

   输入三个整数，保留在变量m、n、p中。

   
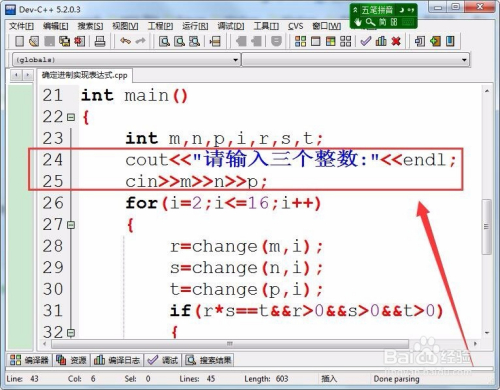
10. 10

    用for轮回节制各进制的计较，进制从2到16。

    
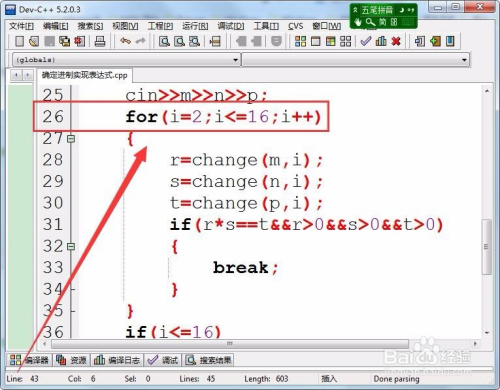
11. 11

    用函数计较各整数对应进制的数值，保留在变量r、s、t中。

    
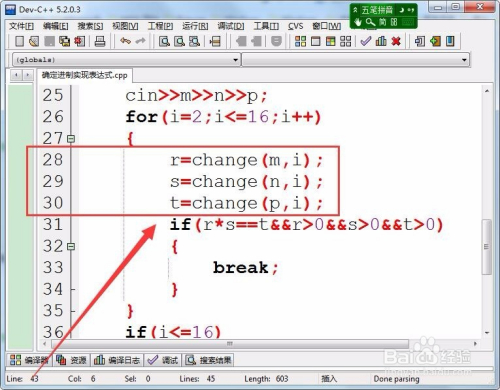
12. 12

    若是等式当作立，且r、s、t的值都年夜于0，则退出轮回。

    
13. 13

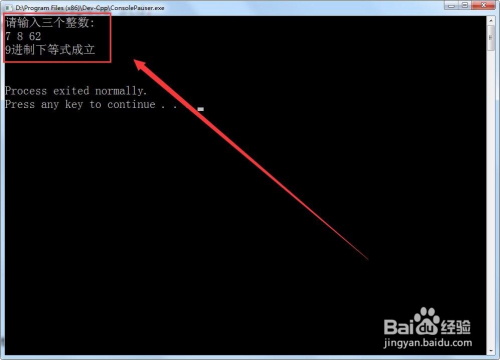
    当等式存在进制的时辰，输出该进制劣等式m×n=p当作立。

    
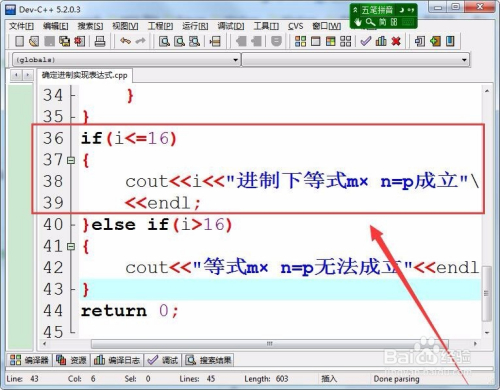
14. 14

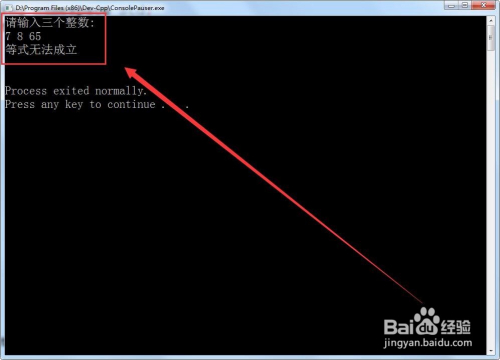
    若是没有等式当作立的进制，则输出等式m×n=p无法当作立。

    
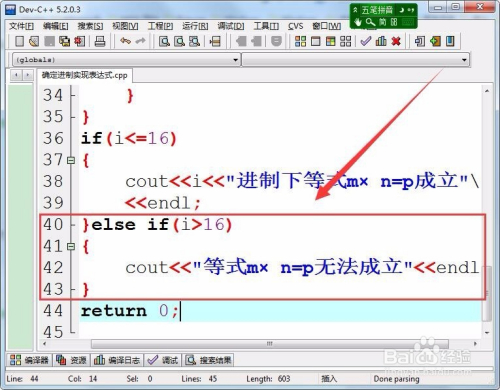
15. 15

    运行法式，输入三个整数后，计较机就会判定该等式有无当作立的进制。